Google Code Jam 2008 – kolo 2
Článek vyšel na serveru Programujte.com.
Google Code Jam pokračuje druhým kolem.
Binární strom
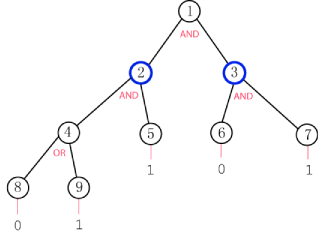 Zadání: Máme binární strom, který má v listech hodnotu
Zadání: Máme binární strom, který má v listech hodnotu 0 nebo 1. V uzlech je buď operátor AND nebo OR s tím, že u některých uzlů je možné operátor prohodit. Naším úkolem je zjistit minimální možný počet změn, který do kořene dostane zadanou hodnotu. Řešení
Při řešení vyjdeme z kořene – pokud je tam operátor AND a my chceme dostat jedničku, tak musíme oba potomky nastavit na jedničku (obdobně pokud je operátor OR a my chceme dostat nulu). V jiném případě stačí nastavit jen jednoho z potomků. Kromě toho ještě vyzkoušíme, jestli by se nevyplatilo operátor v daném uzlu změnit (pokud to jde) a dále pokračujeme rekurzivně. Hodnotu listů už neovlivníme, proto vrátíme buď nulu nebo nekonečno.
<?php /** Určení minimálního počtu změn v binárním stromu * @param bool požadovaná hodnota v kořeni * @param array seznam všech uzlů - array(array("and" => $bool, "changeable" => $bool), ..., array("value" => $bool), ...) * @param int index zkoumaného uzlu * @return int minimální možný počet změn */ function boolean_tree($desired, $nodes, $n = 0) { $node = $nodes[$n]; if (isset($node["value"])) { return ($node["value"] == $desired ? 0 : count($nodes)); } $child1 = boolean_tree($desired, $nodes, 2*$n+1); $child2 = boolean_tree($desired, $nodes, 2*$n+2); if ($desired xor $node["and"]) { return min($child1, $child2); } elseif ($node["changeable"] && ($child1 || $child2)) { return 1 + min($child1, $child2); } return $child1 + $child2; } ?>
Obsah trojúhelníku
Zadání: Naším úkolem je zjistit, jestli existuje trojúhelník s celočíselnými souřadnicemi z daného rozsahu, jehož obsah je zadaný. Řešení
Řešení: Pro výpočet obsahu trojúhelníku použijeme vzorec 1/2 * |xB * yC + xC * yB|. První bod můžeme zafixovat v souřadnici (0, 0), protože trojúhelník jde vždy překlopit tak, aby tam jeden vrchol ležel. Ostatní souřadnice postupně vyzkoušíme:
<?php function triangle_points($n, $m, $a) { if ($a <= $n*$m) { for ($xb=0; $xb <= $n; $xb++) { $xb_yc = 0; for ($yc=1; $yc <= $m; $yc++) { $xb_yc += $xb; $yb_xc = factorization($n, $m, $xb_yc + $a); if ($yb_xc) { return "0 0 $xb $yb_xc $yc"; } if ($xb_yc >= $a) { $yb_xc = factorization($n, $m, $xb_yc - $a); if ($yb_xc) { return "0 0 $xb $yb_xc $yc"; } } } } } return "IMPOSSIBLE"; } ?>
Výraz xB * yC se postupně načítá do proměnné $xb_yc, aby se součin nemusel počítat pořád dokola. Pro všechny kombinace xB a yC se následně hledá celočíselný rozklad $xb_yc + $a a $xb_yc - $a (vyjádření xC * yB z absolutní hodnoty, $a je zadané jako dvojnásobek hledaného obsahu). Pro tento rozklad se používá jednoduchá funkce:
<?php function factorization($n, $m, $a) { static $factorization = array(); if (!isset($factorization[$n][$m][$a])) { $factorization[$n][$m][$a] = ""; for ($yb=ceil($a / $n); $yb <= $m; $yb++) { if ($a % $yb == 0) { $xc = $a / $yb; if ($xc <= $n) { $factorization[$n][$m][$a] = "$yb $xc"; break; } } } } return $factorization[$n][$m][$a]; } ?>
Funkce vrací nalezené souřadnice yB a xC. Aby se celočíselný rozklad nemusel počítat pořád dokola, ukládají se nalezené výsledky do statické proměnné. Funkce by se dala zoptimalizovat tím, že by se hledalo jen v prvočíslech, pro vyřešení příkladu to ale není potřeba.
Hvězdné války
| x | y | z | p |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 1 | 2 | 0 | 1 |
| 3 | 4 | 0 | 1 |
| 2 | 1 | 0 | 1 |
Zadání: Ve vesmíru je rozmístěno několik lodí, z nichž každá má přijímač daného výkonu (u každé lodi může být jiný). Mezi tyto lodě je potřeba umístit vysílač, ze kterého zachytí signál všechny lodě. Naším úkolem je zjistit minimální možný výkon tohoto vysílače, umístit ho můžeme na libovolné místo. Potřebný výkon vysílače je definován jako (|xi – x| + |yi – y| + |zi – z|) / pi, kde (x, y, z) je umístění vysílače a (xi, yi, zi, pi) je umístění a výkon přijímače jednotlivých lodí. Řešení
Řešení této úlohy je triviální. Jak bychom postupovali, pokud by všechny lodě ležely na přímce? Jednoduše bychom vzali dvě nejvzdálenější lodě (se zohledněním výkonu jejich přijímače) a mezi ně bychom umístili vysílač. V definované metrice je to totéž – paprsek může létat pouze po rovnoběžkách s osami souřadného systému. Dokonce se ani nemusíme zatěžovat s určováním pozice vysílače (ten může ležet někde na ploše mezi dvěma nejvzdálenějšími body).
<?php /** Určení výkonu vysílače, ze kterého signál dojde ke všem lodím * @param array souřadnice a výkony lodí - array(array($x, $y, $z, $p), ...) * @return float minimální možný výkon vysílače */ function cruiser($ships) { $return = 0; foreach ($ships as $ship1) { foreach ($ships as $ship2) { $return = max($return, (abs($ship2[0] - $ship1[0]) + abs($ship2[1] - $ship1[1]) + abs($ship2[2] - $ship1[2])) / ($ship2[3] + $ship1[3])); } } return $return; } ?>
Přestože se řešení úlohy vejde na tři řádky, přišla mi úloha nejsložitější ze všech a také jsem jejím řešením strávil nejvíc času. Původně jsem totiž nevěnoval pozornost vzorci pro výpočet potřebného výkonu a měl jsem za to, že se používá běžná euklidovská geometrie (takže paprsek může letět přímo). To by znamenalo kolem všech lodí obalit minimální možnou kouli, což je doslova o dva řády náročnější úloha.
RLE permutace
| Permutace | Vstup | Výstup |
|---|---|---|
| 3, 1, 2, 4 | abcd | cabd |
Zadání: Máme algoritmus, který nejprve provede permutaci nad bajty zadaného vstupu a potom výsledek zkomprimuje algoritmem RLE. Naším úkolem je navrhnout permutaci dané délky, která pro zadaný vstup vrátí co nejmenší počet skupin stejných bajtů (jedná se o zjednodušení algoritmu RLE), a vrátit tento počet. Např. v posloupnosti aaaabbcaaa jsou čtyři skupiny stejných bajtů. Řešení
Řešení: Přímočaré řešení spočívá ve vyzkoušení všech permutací dané délky:
<?php function perm_rle($s, $k, $perm = array()) { if (!$k) { $return = 0; $prev = ""; for ($i=0; $i < strlen($s); $i += count($perm)) { foreach ($perm as $val) { if ($prev != $s[$i+$val]) { $return++; $prev = $s[$i+$val]; } } } return $return; } $return = strlen($s); foreach ($k as $val) { $return = min($return, perm_rle($s, array_diff($k, array($val)), array_merge($perm, array($val)))); } return $return; } ?>
Toto řešení se nicméně nedá použít pro velký vstup, kde můžou mít permutace délku až 16.
Diskuse
honza:
tohle jsou dost zajímavý úlohy, tak nějak jsem doufal že tohle v php nebude :D nikdy mi nešly tyhle úlohy....
Tom:
Tyhle úlohy ani tak nesouvisí s PHP, jako spíš s logickým myšlením a schopností z textového zadání sestavit vzorec/postup.Tohle bych spíš než na Google Jam očekával na IQ testech, nebo tak něčem...
Diskuse je zrušena z důvodu spamu.

