Google Code Jam 2008 – kvalifikace
Článek vyšel na serveru Programujte.com.
Google Code Jam po cvičení pokračuje kvalifikací.
Přepínání vyhledávačů
| Dotazy |
|---|
| Yeehaw Yeehaw Googol B9 Googol NSM B9 NSM Dont Ask Googol |
| Vyhledávače |
|---|
| Yeehaw NSM Dont Ask B9 Googol |
Zadání: Věděli jste, že když do vyhledávače Google zadáte „Google“, tak se zhroutí vesmír? Tedy ne v naší realitě, ale v nějaké alternativní. Proto byl navržen centrální systém, který zpracovává všechny dotazy a rozděluje je mezi jednotlivé vyhledávače tak, aby ke zhroucení vesmíru nedošlo. Změna vyhledávače je náročná, proto je naším cílem počet těchto přepnutí minimalizovat. Úkolem úlohy je ze zadaného seznamu vyhledávačů a dotazů zjistit minimální možný počet přepnutí (neboli zjistit, jakých vyhledávačů a v jakém pořadí se máme dotázat). Řešení
Řešení: Bohužel nejde použít hladový algoritmus, protože dlouhá posloupnost ukrojená na začátku by nám mohla zkomplikovat situaci v budoucnu. Proto raději vyzkoušíme všechny možnosti:
<?php function switches($engines, $queries, &$switches_queries = array()) { $min_switches = null; foreach ($engines as $engine) { $pos = array_search($engine, $queries); if ($pos === false) { return 0; } elseif ($pos) { $switches = &$switches_queries[count($queries) - $pos][$engine]; if (!isset($switches)) { $switches = switches($engines, array_slice($queries, $pos), $switches_queries); } if (!isset($min_switches) || $min_switches > $switches) { $min_switches = $switches + 1; } } } return $min_switches; } ?>
V kódu je použitá funkce array_search, která mezi dotazy hledá název aktuálního vyhledávače. Pokud ho nenajde, tak jsme hotovi, protože pro zbylé dotazy už vyhledávač nemusíme měnit. Pokud ho naopak najdeme hned na začátku, tak už nic nezkoušíme, protože bychom se dostali do nekonečné smyčky. V jiných případech vyzkoušíme pro zbylé dotazy všechny vyhledávače.
Stejně jako u pouštění vajíček se používá dynamické programování, abychom nemuseli kratší posloupnosti počítat pořád dokola. Keš ale nedržíme ve statické proměnné, protože po sobě následující úlohy mohou používat různé vyhledávače, pro které se počet změn samozřejmě může lišit. Místo toho se používá parametr předávaný referencí inicializovaný na prázdné pole (což je možné od PHP 5), kterému bohužel v PHP nejde určit výchozí hodnota, takže je před zavoláním fukce potřeba tuto proměnnou nainicializovat na prázdné pole (mohla by to dělat obálková funkce).
Jízdní řád
| Zastávka B | |
|---|---|
| 12:02 | 15:05 |
| 09:00 | 10:35 |
| Zastávka A | |
|---|---|
| 09:00 | 12:05 |
| 10:00 | 13:05 |
| 11:00 | 12:35 |
Zadání: Vlaková trať má dvě zastávky A a B. Vlaky po trati jezdí podle jízdního řádu. Vlaky jezdí různou rychlostí a na trati se mohou předjíždět. Vlaky nezajíždí do jiných zastávek a nemohou jezdit mimo jízdní řád. Naším úkolem je zjistit, kolik vlaků musí dopravce ráno připravit do obou zastávek, aby mohly jezdit podle jízdního řádu. Řešení
Řešení je přímočaré:
<?php /** Výpočet počtu vlaků potřebných v jednotlivých stanicích * @param array pole s prvky $departure_time => array(array("from" => $station, "arrival" => $arrival_time), ...), časy zadané v minutách * @return array dvouprvkové pole s potřebnými počty vlaků v jednotlivých stanicích */ function timetable($departures) { $needed = array(0, 0); $going = array(); $available = array(0, 0); ksort($departures); foreach ($departures as $departure => $trains) { foreach ($going as $key => $train) { if ($train["arrival"] <= $departure) { $available[1 - $train["from"]]++; unset($going[$key]); } } foreach ($trains as $train) { if (!$available[$train["from"]]) { $needed[$train["from"]]++; } else { $available[$train["from"]]--; } $going[] = $train; } } return $needed; } ?>
Projdeme seznam všech odjezdů a pro každý nejprve zjistíme, jestli už se nevrátil nějaký vlak. Potom pro všechny vlaky odjíždějící v daný čas zjistíme, jestli v zastávce máme k dispozici nějakou soupravu ($available) a pokud ne, tak si poznamenáme, že budeme potřebovat o jednu navíc ($needed). Aktuální vlak si přidáme do jedoucích vlaků ($going).
Plácačka na mouchy
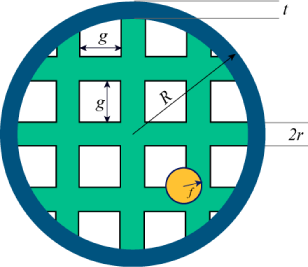 Zadání: Mějme kruhovou tenisovou raketu bez rukojeti s rámem a výpletem začínajícím ve středu rakety. Touto raketou se snažíme trefit mouchu. Zadaný je poloměr mouchy, poloměr rakety, šířka rámu, poloměr výpletových vláken a jejich rozestup. Naším úkolem je zjistit, jaká je pravděpodobnost trefení mouchy, pokud moucha letí na náhodném místě a svým středem vždy letí uvnitř vnějšího okraje rakety. Řešení
Zadání: Mějme kruhovou tenisovou raketu bez rukojeti s rámem a výpletem začínajícím ve středu rakety. Touto raketou se snažíme trefit mouchu. Zadaný je poloměr mouchy, poloměr rakety, šířka rámu, poloměr výpletových vláken a jejich rozestup. Naším úkolem je zjistit, jaká je pravděpodobnost trefení mouchy, pokud moucha letí na náhodném místě a svým středem vždy letí uvnitř vnějšího okraje rakety. Řešení
K řešení úlohy lze přistoupit několika způsoby. Jednak můžeme pravděpodobnost přesně vypočítat jako poměr obsahu volné plochy a plochy celé rakety (se zohledněním mouchy), to je ale poměrně pracné. Druhou možností je raketu bombardovat náhodnými mouchami a vždycky jen zjistit, jestli raketu trefila:
<?php define("TRIES", 1e6); define("MT_RAND_MAX", mt_getrandmax()); function swatter_string($x, $f, $r, $g) { $center = round($x / ($g+2*$r)) * ($g+2*$r); return ($x > $center - $r - $f && $x < $center + $r + $f); } function swatter_rand($f, $R, $t, $r, $g) { $hits = 0; $tries = 0; for ($i=0; $i < TRIES; $i++) { $x = $R * mt_rand() / MT_RAND_MAX; $y = $R * mt_rand() / MT_RAND_MAX; $distance = $x*$x + $y*$y; if ($distance < $R*$R) { $tries++; if ($distance > ($R-$t-$f) * ($R-$t-$f) || swatter_string($x, $f, $r, $g) || swatter_string($y, $f, $r, $g)) { $hits++; } } } return $hits / $tries; } ?>
Postupně generujeme dvojice náhodných čísel pro souřadnice X a Y. Pokud splňují podmínku, že jsou uvnitř rakety, tak zjistíme, jestli strefí rám rakety nebo svislá či vodorovná lanka výpletu. Nakonec jen vrátíme poměr tref a počtu úspěšných pokusů. Problém tohoto přístupu spočívá v tom, že úplné zadání toleruje absolutní nebo relativní chybu jen 10-6, pro jejíž dosažení bychom museli provést tolik pokusů, že by skript běžel neúměrně dlouho.
Proto vyzkoušíme ještě jedno řešení, nazveme ho numerické. Budeme postupovat po ose Y a v každém bodě zjistíme šířku rakety a šířku překážek na raketě v daném bodě.
<?php function swatter_numeric($f, $R, $t, $r, $g) { if ($g <= 2*$f) { return 1; } $hits = 0; $tries = 0; $R_in = $R-$t-$f; $y_center = 0; for ($y=$R/TRIES; $y < $R; $y += $R/TRIES) { if ($y - $y_center >= $g/2+$r) { $y_center += $g+2*$r; } $tries += sqrt($R*$R - $y*$y); if ($y < $R_in && ($y < $y_center - $r - $f || $y > $y_center + $r + $f)) { $x = sqrt($R_in*$R_in - $y*$y); $squares = (int) (($x+$f+$r) / ($g+2*$r)); $hits += $squares * ($g-2*$f); $hits += max(0, $x - $squares * ($g+2*$r) - $r - $f); } } return 1 - $hits / $tries; } ?>
Diskuse
Gimli2:
Nastin analytickeho reseni placacky na mouchy. Predstava vychazi z nacrtku: http://img518.imageshack.us/img518/9184/placackanamouchufj5.jpg (cely pripad budeme reset jen na 1/4 kruhu, protoze pomer ploch a tedy i sance zasazeni mochy bude stejna)
Sance, ze moucha proleti je pomer zlute ku zelene plose (napr. X) na stretim obrazku. Trefeni je tedy pravdepodobne s P = 1-X.
Aby moucha zasazena nebyla, musi mit svuj stred dostatecne daleko od hran vypletu a samotne rakety. Na prvnim z obrazku jsou to ta bila mista.
Vyuzijeme logicke operace rozdil nad plosnymi objekty. Od zlute kruznice (s polomerem R-t-f) postupne odecteme svisle a lezate obdelniky o rozmeru 2(r+f)×(R-t-f). Vzdalenost mezi jejich stredy je g+2r. A cele jsou posunuty o r+f doleva. Z prvniho zleva a zespodu je tak vlastne jen pulka.
Plosny objekt muze byt reprezentovan mnozinou bodu a mnozinou jejich spojnic. Kazda spojnice muze byt bud usecka, nebo oblouk z kruznice s polomerem R-t-f a stredem v pocatku souradnic. Objekt nemusi byt souvisly. Pak jeho casti nazyvejme treba subobjekty.
Kazdy subobjekt (ctverecek ve vypletu, pripadne serizly kruznici) bude mit 3 nebo 4 vrcholy a 4 nebo 3 usecky a 0 nebo 1 oblouk.
Pro samotny vypocet rozdilu spocitame prusecik dane kruznice s obdelnikem (pro svisle budou pruseciky jen na svislych stranach, nebo ve vrcholech; pro lezate to bude analogicky). Tim se nam definuji 4(3) body/vrcholy vznikleho subobjektu a vime, ze spojnice tech 2 pruseciku bude obloukem, ostatni spojnice useckou. Ale logicky rozdil vektorovych objektu uz urcite budou hotove a rychle algoritmy. ;-)
Na zaver bude jen potreba spocitat plochy. Zelena ctvrtkruznice ma plochu 1/4×Pi×(R+f)^2. U zluteho objektu je potreba spocita sumu ploch jednotlivych subobjektu. Ctverecky jsou jasne (pozname je ze nemaji ani jednu spojnici typu oblouk). A serizle ctverecky vypocitame s pomoci integralu jako plochu pod grafem rezajici kruzice zmensenou o obdelnik o sirce nejsirsiho mista subobjektu a vysce od osy x po spodni usecku subobjektu.
Prgat se mi to nechce ;-), ale pokud by clovek nasel hotove reseni rozdilu plosnych objektu, byla by to prace na okamzik...
 Jakub Vrána
Jakub Vrána  :
:
Myšlenkový pochod je správný, prošel jsem ho stejně. Bavit mě tohle řešení přestalo v momentě, kdy bylo potřeba u každého čtverce vypočítat 4 průsečíky s kružnicí (to by ještě šlo) a potom spočítat plochu těch zaoblených trojúhelníků (jeho obsah je součet obsahu trojúhelníku a kruhové úseče).
Taky se mi to nechtělo programovat :-).
 Jakub Vrána
Jakub Vrána  :
:
Tady je kód:
<?php
function swatter_compute($f, $R, $t, $r, $g) {
$blank = 0;
$R2 = ($R-$t-$f) * ($R-$t-$f);
for ($x1 = $r+$f; $x1 < $R-$t-$f; $x1 += $g+2*$r) {
// 1 left, 2 right, 3 top, 4 bottom
$x2 = $x1 + $g - 2*$f;
$y1 = sqrt($R2 - $x1*$x1);
$y2 = ($x2 < $R-$t-$f ? sqrt($R2 - $x2*$x2) : -$r-$f);
$squares1 = floor(($y1-$r-$f) / ($g+2*$r));
$squares2 = floor(($y2+$r+$f) / ($g+2*$r));
$blank += $squares2 * ($g-2*$f) * ($g-2*$f);
for ($squares=$squares1; $squares >= $squares2; $squares--) {
$x3 = $x1;
$y3 = $y1;
if ($y1 > $squares * ($g+2*$r) + $r+$g-$f) {
$y3 = $squares * ($g+2*$r) + $r+$g-$f;
$x3 = sqrt($R2 - $y3*$y3);
$blank += ($g - 2*$f) * ($x3 - $x1);
}
$x4 = $x2;
$y4 = $y2;
if ($y2 < $squares * ($g+2*$r) + $r+$f) {
$y4 = $squares * ($g+2*$r) + $r+$f;
$x4 = sqrt($R2 - $y4*$y4);
} else {
$blank += ($x2 - $x3) * ($y2 - $squares * ($g+2*$r) - $r-$f);
}
$blank += ($x4-$x3) * ($y3-$y4) / 2;
$distance = sqrt(($x4-$x3) * ($x4-$x3) + ($y3-$y4) * ($y3-$y4));
$alpha = asin($distance/2 / ($R-$t-$f));
$blank += $R2 * ($alpha - cos($alpha) * sin($alpha));
}
}
return 1 - 4 * $blank / (M_PI*$R*$R);
}
?>
Na malý vstup mi funguje, na velký bohužel ne. Nevím, jestli to je jen nedostatečnou přesností nebo nějakou chybou.
 Jakub Vrána
Jakub Vrána  :
:
Jediná komplikace byla v neošetření okrajové podmínky. Takže stačí na začátek funkce přidat <?php if ($g < 2*$f) return 1; ?> a už to správně funguje i pro velký vstup – sláva!
Diskuse je zrušena z důvodu spamu.

